Training Compute-Optimal Large Language Models
Summary
Optimal model size and number of tokens is fixed with the compute budget.
What is found is that model size N and numbe of tokens D should scale equally.
\( 2 \times N \implies 2 \times D \)
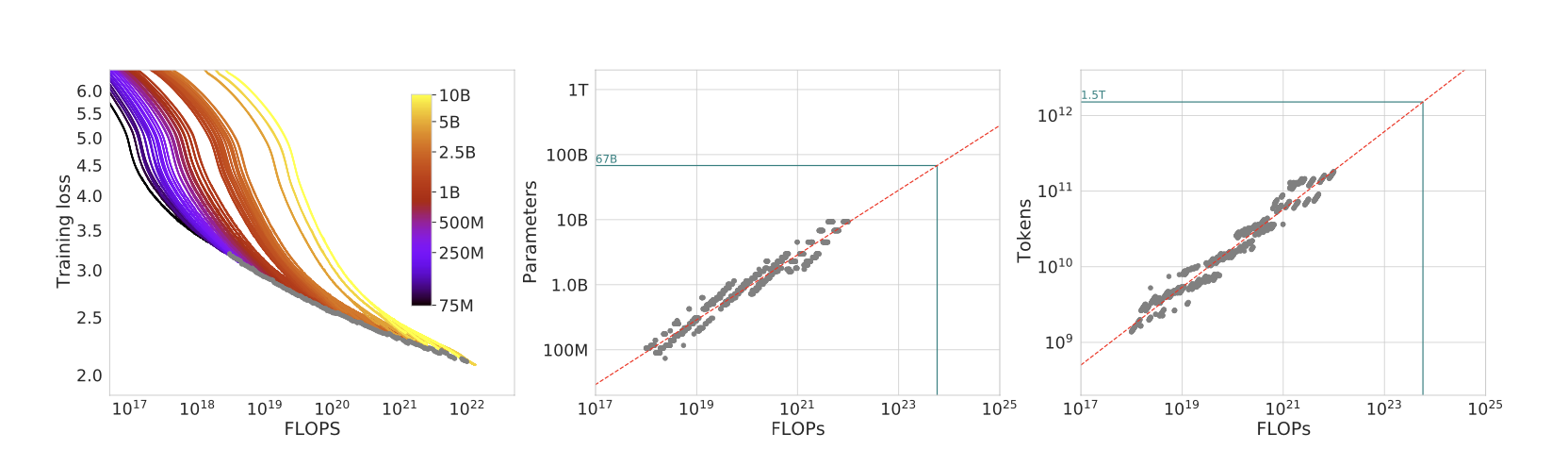
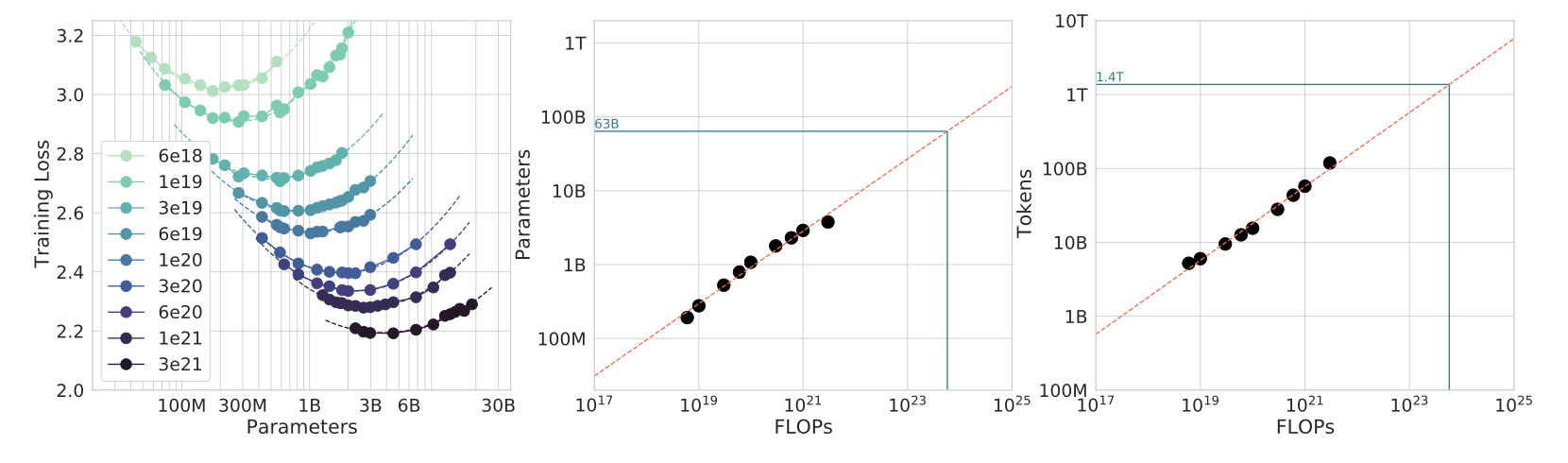
Given a fixed FLOPs budget, how should we tradeoff model size N and training tokens D?
- Fix N and vary D (from 70M to 10B)
- Fix D and vary N (create 16 FLOPs curves (isoFLOPs))
- Fitting a parametric loss function: model all losses as parametric functions of N and D
\( \hat{L}(N, D) = E + \frac{A}{N^{\alpha}} + \frac{B}{N{\beta}}\)
where \(E\) is the entropy of natural text, the second term indicates how a transformer with N parameters still underperforms, and the third term is the finite number of optimization steps.
This function can be optimized with Huber loss, creating M isoFLOPs slices and isoLoss contours.
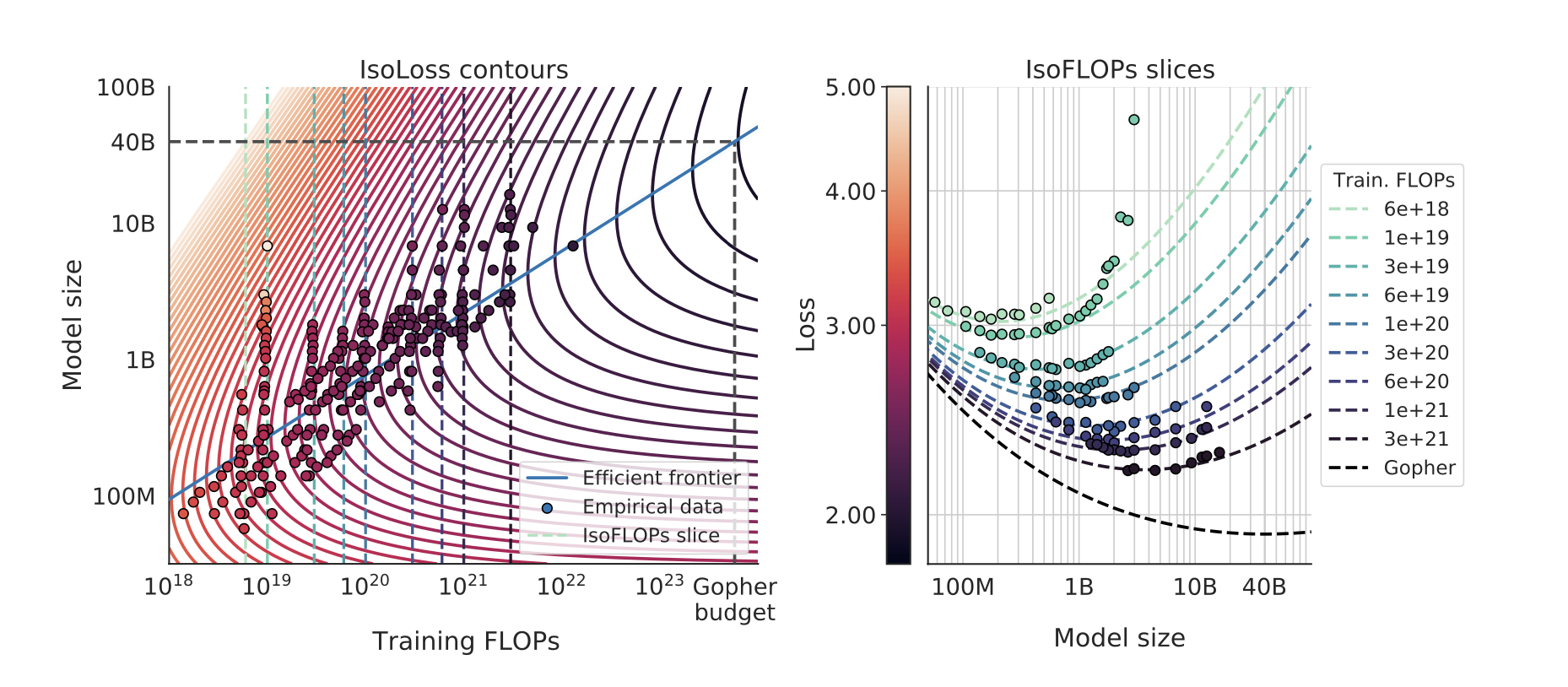
Optimal model scaling?
All three approaches yield the same optimal scaling law: to keep C constant, N and D have to scale in a proportional way.